Statistischer Rückenwind - Stichprobengrößen im A/B-Testing

A/B-Tests helfen dabei, zwei Varianten einer bestimmten Komponente zu vergleichen. Dabei ist das Ziel, die Variante zu finden, die beim Kunden zu mehr Interaktion führt.

So können beispielsweise verschiedene Werbebanner verglichen werden, um die Klickrate zu maximieren oder verschiedene Webpages, mit dem Ziel die Kunden länger auf der Website zu halten. Üblich ist es auch, A/B-Test für Emails einzusetzen. Hier kann interessant sein, ob eine andere Betreffzeile zu einer höheren Öffnungsrate oder eine anderes gestalteter Inhalt zu einer höheren Klickrate führen.

Das Vorgehen ist in allen Fällen ähnlich:

1. zunächst werden (mind.) zwei Varianten des zu testenden Objekts erstellt
2. dann werden zwei getrennte Testgruppen, die Teil der Grundgesamtheit sind, mit Variante A oder mit Variante B konfrontiert
3. statistische Tests zeigen dann, welche der Varianten eine größeren Einfluss auf die Zielgröße hat.

Die "Gewinner"-Variante wird allen nachfolgenden Besuchern angezeigt. Bei Emails erhalten alle restlichen Abonnenten, die nicht zu einer der Testgruppen gehört haben, die Gewinner-E-Mail.

Das Problem der fehlenden Basis

Die Reaktionen der Mitglieder der (Test-)Gruppen versucht man dabei zu verallgemeinern. In der Statistik nennt man die Gruppen „Stichproben“. Wenn sich die Ergebnisse tatsächlich verallgemeinern lassen, spricht man davon, dass sie „repräsentativ“ für alle Personen sind – also für die Grundgesamtheit gelten.

Betrachtet man die Aussagekraft der Testergebnisse durch die Brille der Statistik, stellt man leider häufig fest, dass die gefällte Entscheidung eher ein Ratespiel war und eben nicht belastbar ist.

Um ein repräsentatives, statistisch signifikantes Ergebnis zu erhalten, kommt es auf die Anzahl der Testpersonen an, welche häufig unterschätzt wird. Daher die entscheidende Frage: Wie groß muss meine Stichprobengröße pro Variante sein, um sicher einen Gewinner küren zu können?

Statt sich nun den Kopf über komplexen Formeln zu zerbrechen, können wir praktischerweise auf simple Online-Rechner zurückgreifen, die wir im Folgenden auch noch besprechen werden. Um sie verstehen zu können, bedarf es allerdings noch ein paar weniger statistischer Begrifflichkeiten.

Vier statistische Vokabeln für Ihren erfolgreichen Tests

Die Stichprobengröße hängt von vier Variablen ab: der erwarteten Konversionsrate, der minimalen Effektgröße, der Teststärke sowie der Irrtumswahrscheinlichkeit.

• Die erwartete Konversionsrate (engl.: Baseline conversion rate) gibt den prozentualen Anteil der Besucher bzw. Kunden an, die eine gewünschte Handlung ausführen. Angenommen wir verschicken 1000 E-Mails und 300 E-Mails werden geöffnet, so liegt die Konversionsrate für das Öffnen der E-Mail bei 30%. Diese Variable wird aufgrund von Erfahrungen und Erwartungen geschätzt.
• Die minimale Effektgröße (engl.: Minimum Detectable Effect) gibt an, um wieviel Prozent, die eine Variante besser oder schlechter sein müsste, damit der Test als statistisch signifikant eingestuft wird. Es gilt die Faustregel: Je kleiner die minimale Effektgröße, desto größer die Stichprobengröße. Diese Variable kann und sollte, je nach Kapazität, verändert werden. Sie kann entweder in absoluten oder relativen Prozenten angegeben werden.
• Die Wahrscheinlichkeit, mit der ein signifikanter Unterschied erkannt wird, obwohl keiner existiert, wird Irrtumswahrscheinlichkeit (engl.: Significance level) genannt. In der Regel wird ein Wert von 5% gesetzt.
• Die Teststärke (engl.: Statistical power) definiert, mit welcher Wahrscheinlichkeit ein existierender Unterschied zwischen den Varianten erkannt wird. Der Standard liegt hier bei 80%. Sowohl die Irrtumswahrscheinlichkeit als auch die Teststärke sollten nach Möglichkeit nicht stark verändert werden.

Berechnen der Stichprobengröße

Wie schon angekündigt greifen wir auf bequeme Online-Tools zurück. Ein empfehlenswerter Rechner ist der von Evan Miller. Hier finden wir die vier Variablen wieder und können diese einfach einsetzten. Der Rechner gibt uns dann die Anzahl der benötigten Impressionen pro Variante an, damit unser A/B-Test einen statistisch signifikanten Gewinner hervorbringen kann.

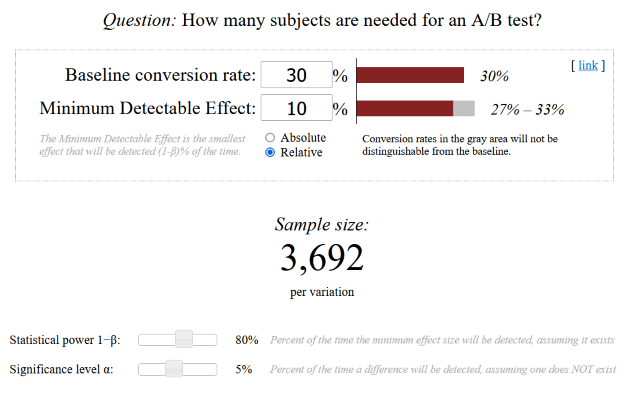
Um ein Gefühl für die Größenordnungen und Zusammenhänge zu bekommen, können wir die Formeln graphisch abschätzen.

Die verschiedenen Graphen stehen für verschiedene Konversionsraten. Auf der x-Achse finden wir die minimale relative Effektgröße und können demnach auf der y-Achse die Stichprobengröße pro Variante ablesen. Die Teststärke liegt bei 80%, die Irrtumswahrscheinlichkeit bei 5%.

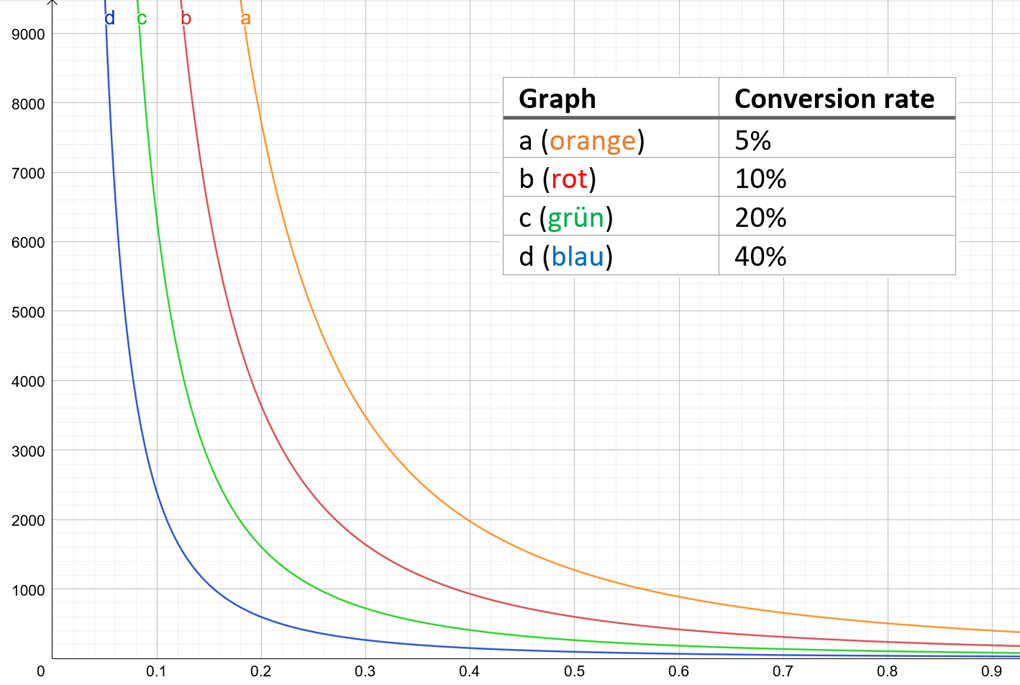
Hinweise und Schwierigkeiten

Wie bei allen statistischen Tests gibt es Faktoren, die extern auf unser Ergebnis einwirken und es unter Umständen verfälschen könnten. Das können saisonale Schwankungen, Pausen- und Urlaubszeiten oder aber auch das Verhalten der Konkurrenz sein. Es gilt diese externen Faktoren abzuschätzen und mit einfließen zu lassen.

Trotz des theoretischen Hintergrunds der Stichprobengröße in A/B-Tests können in der Praxis A/B-Tests durchgeführt werden, auch wenn sie nicht statistisch signifikant sind – denn es gilt: schwache Daten sind immer noch besser als gar keine.

Das könnte Sie auch interessieren: